上海2020-2021学年松江一中高中二年级上学期数学期中考试
考生注意:
本卷满分150分,考试时间120分钟,答案全部做在答卷纸上
1、填空题(本大题共有12题,满分54分考生需要在答卷纸相应编号的空格内直接填写结果,第1~6题每一个空格填对得4分,第7~12题每一个空格填对得5分,不然一律得零分).
1.过点![]() ,且法向量是
,且法向量是![]() 的直线的点法向式方程是__________.
的直线的点法向式方程是__________.
2.若线性方程组的增广矩阵为![]() ,解为
,解为![]() ,则
,则![]() __________.
__________.
3.行列式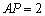 中,第2行第1列元素的余子式的值为10,则实数
中,第2行第1列元素的余子式的值为10,则实数![]() __________.
__________.
4.直线![]() 过点
过点![]() 且在两坐标轴上的截距相等,则直线
且在两坐标轴上的截距相等,则直线![]() 方程是__________.
方程是__________.
5.设无穷等比数列![]() 的公比为
的公比为![]() ,若
,若![]() ,则
,则![]() __________.
__________.
6.直线![]() 与直线
与直线![]() 互相垂直,则实数
互相垂直,则实数![]() __________.
__________.
7.![]() ,直线
,直线![]() 过定点_________________.
过定点_________________.
8.用数学总结法证明![]() 的过程中,从
的过程中,从![]() 到
到![]() 时,
时,![]() 比
比![]() 共增加了___________项.
共增加了___________项.
9.若直线![]() 过点
过点![]() ,且与直线
,且与直线![]() 的夹角为
的夹角为![]() ,则直线
,则直线![]() 的一般式方程是____________________.
的一般式方程是____________________.
10.设![]() 的倾斜角为
的倾斜角为![]() 绕其上一点
绕其上一点![]() 沿逆时针方向旋转
沿逆时针方向旋转![]() 角得到直线
角得到直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() 绕
绕![]() 沿逆时针方向再旋转
沿逆时针方向再旋转![]() 角得到直线
角得到直线![]() ,则
,则![]() 的方程为_______________.
的方程为_______________.
11.在平面直角坐标系中,概念![]() 为
为![]() 两点之间的“折线距离”。则原点
两点之间的“折线距离”。则原点![]() 与直线
与直线![]() 上一点
上一点![]() 的“折线距离”的最小值是___________.
的“折线距离”的最小值是___________.
12.设![]() 为
为![]() 的内心,三边长
的内心,三边长![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,若直线
,若直线![]() 交直线
交直线![]() 于点
于点![]() ,则线段
,则线段![]() 的长为_____________.
的长为_____________.
2、选择题(本大题共有4题,满分20分,每题5分),每题有且只有一个正确答案,考生需要在答卷纸相应地方上,将代表答案的小方格涂黑.
13.已知直线![]() 与直线
与直线![]() ,那样“
,那样“![]() ”是“
”是“![]() ”的( )
”的( )
A.充分非必要条件 B.必要不充分条件 C.充要条件 D.既不充分也非必要条件
14.已知点![]() 与点
与点![]() 关于直线
关于直线![]() ,则点
,则点![]() 的坐标是( )
的坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
15.已知![]() 是两个非零向量,若函数
是两个非零向量,若函数![]() 的图像是一条直线,则必有( )
的图像是一条直线,则必有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
16.已知点![]() 与点
与点![]() 在直线
在直线![]() 的两侧,给出以下结论:①
的两侧,给出以下结论:①![]() ;②当
;②当![]() 时,
时,![]() 有最小值,无最大值;③
有最小值,无最大值;③![]() ;④当
;④当![]() 且
且![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ,正确的个数为( )
,正确的个数为( )
A.1个 B.2个 C.3个 D.以上都不对
3、解答卷(本大题共有5题,满分76分)解答下列各题需要在答卷纸相应编号的规定地区内写出必要的步骤.
17.(本题满分14分)
已知直线![]() ,直线
,直线![]() ,用行列式求:当
,用行列式求:当![]() 为什么值时,直线
为什么值时,直线![]() 与
与![]() 分别有如下地方关系:相交并求出交点;平行;重合.
分别有如下地方关系:相交并求出交点;平行;重合.
18.(本题满分14分)
已知![]() 为坐标原点,设
为坐标原点,设![]()
(1)求![]() 的面积
的面积![]() ;
;
(2)对向量![]() ,概念
,概念![]() ,
,![]() ,并说明
,并说明![]() 与
与![]() 的关系:
的关系:
(3)请总结![]() 的几何意义.
的几何意义.
19.(本题满分14分)
已知直线![]() ,直线
,直线![]() 和直线
和直线![]() ,且
,且![]() 与
与![]() 的距离是
的距离是![]() .
.
(1)求![]() 的值;
的值;
(2)能否找到一点![]() ,使得
,使得![]() 点同时满足下列三个条件:①
点同时满足下列三个条件:①![]() 是第一象限的点;②
是第一象限的点;②![]() 点到
点到![]() 的距离是
的距离是![]() 点到
点到![]() 的距离的
的距离的![]() ;③
;③![]() 点到
点到![]() 的距离与
的距离与![]() 点到
点到![]() 的距离之比是
的距离之比是![]() .若能,求
.若能,求![]() 点坐标;若不可以,说明理由.
点坐标;若不可以,说明理由.
20.(本题满分16分)
已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,集合
,集合![]() ,集合
,集合![]() ,请判断下列三个命题的真伪。若为真,请给予证明;若为假,请举出反例.
,请判断下列三个命题的真伪。若为真,请给予证明;若为假,请举出反例.
(1)以集合![]() 中的元素为坐标的点均在同一条直线上;
中的元素为坐标的点均在同一条直线上;
(2)当![]() 时,
时,![]() 肯定为空集;
肯定为空集;
(3)当![]() 时,
时,![]() 只含有一个元素.
只含有一个元素.
21.(本题满分18分)
如图所示,将一块直角三角形板![]() 置于平面直角坐标系中,已知
置于平面直角坐标系中,已知![]() ,点
,点![]() 是三角板内一点,现因三角板中,阴影部分遭到损毁,要把损毁部分锯掉,可用经过点
是三角板内一点,现因三角板中,阴影部分遭到损毁,要把损毁部分锯掉,可用经过点![]() 的任一直线
的任一直线![]() 将三角板锯成
将三角板锯成![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() .
.
(1)用![]() 表示出直线
表示出直线![]() 的方程,并求出点
的方程,并求出点![]() 的坐标;
的坐标;
(2)求出![]() 的取值范围及其所对应的倾斜角
的取值范围及其所对应的倾斜角![]() 的范围;
的范围;
(3)求![]() 面积的取值范围.
面积的取值范围.







